Filter란?
filter는 일상에서 사용하는 용어로 생각해 보면 미세먼지를 걸러 준다거나 기준에 맞지 않는 단어들을 없앤다는 의미를 가진다. 여기서 불필요한 잡음을 걸러내 준다 라고 생각 되지만 반대로 우리가 원하는 것을 얻게 해준다는 개념을 이해 할 수 있다.
data가 들어 왔을 때, noise를 제거하고 원하는 값을 도출해 내는게 Filter이다.
Mean Filter
일반적으로 noise가 있는 data에서 생각 할 수 있는 filter는 평균을 이용하는 것이다. 예를 들어 n개의 data가 있을 때, 식은 다음과 같이 쓸 수 있다.

하지만 로봇에서는 센서 값이 실시간으로 들어오기 때문에 이산 신호 식으로 바꾸면 다음과 같다.
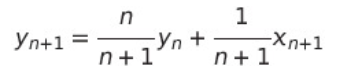
평균 필터의 성능 확인은 다음과 같다.

여기서 기억하고 가야할 식이 바로 다음이다.

이 수식은 뒤에 나올 Low Pass filter와 연관 되어 있는 식이므로, 뒤에서 추가 설명 하겠다.
Code 구현
code 구현은 사실 간단하다. 다음과 같이 하면 된다.

단점
mean filter는 계속 평균을 내는 것이기 때문에 신호가 sin파 같은 게 입력되면 그냥 0으로 수렴해 버리기 때문에 일정한 값이 들어오는 상황에서 noise가 발생할 때 사용하는 것이 바람직 하다.

Move Average Filter(이동 평균 필터)
move average filter는 mean filter의 단점을 좀더 보완 한 것으로, 최근 k개의 data만 평균을 내는 것이다.
이를 이산 신호 식으로 나타내면 다음과 같다.

Move Average Filter의 성능은 다음과 같다.

깔끔하지는 않지만 어느정도 필터링 되는 모습이다.
Code 구현

Low Pass Filter
Low Pass Filter는 주파수 영역대를 제거하는 필터로 일단 회로로 나타내면 다음과 같다.
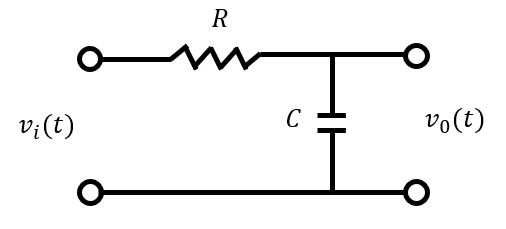
이 회로에서 input , output의 상관 관계를 식으로 적으면 다음과 같다.

이를 라플라스 변환하여 식을 적어보면 다음과 같게 된다.

여기서 Wc는 cutting frequency가 된다. 한마디로 주파수가 급격하게 차단 되는 시점이며 τ는 시상수를 의미한다. 이를 코딩하기 위해 이산 신호 식으로 다시 적으면 다음과 같이 된다.

여기서 최종으로 얻어낸 식이 아래와 같다.

여기서 2번째 식은 위에서 mean filter에서 봤던 식과 같은 식이다. mean filter는 결국 low pass filter와 같은 형식의 filter지만 시간이 지남에 따라 차단 주파수가 달라지는 필터였다.
그러면 α를 어떻게 정하는지는 다음을 보면 된다.

만약 원래 data가 0.1Hz이고, 셈플링 시간이 1초일 때의 filter를 설계하면 τ은 다음과 같이 선정 할 수 있다.
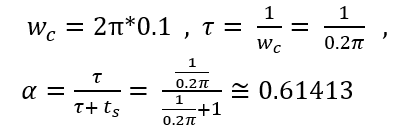
이제 이 값을 이용하여 filter를 적용하면 다음과 같다.

Code 구현

High Pass Filter
High Pass Filter 또한 Low Pass Filter와 마찬가지로 회로에서 이산 신호식을 유도하면 된다. 중간 과정을 생략하고 결과 값만 가져오면 다음과 같다.

이를 low pass filter에서 제거했던 noise를 추출하기 위해 사용하면 다음과 같다.

Code 구현

주파수 필터의 문제점
여기서 주파수 필터의 문제점은 가속도를 적분하여 속도를 얻거나 속도를 적분하여 위치를 얻어낼 때는 사용하기 힘들다는 것이다. 가속도를 예시를 들면, 단순 센서의 offset으로 값이 들어오는 건지, 등가속도로 인해 값이 일정하게 들어오는 것인지 구분을 하지 못한다.
이러한 단점을 보완해 주는 Kalman filter , Extended Kalman filter등이 존재하나 다음 포스팅에 다루겠다.
'통신 & 필터' 카테고리의 다른 글
| [ UART ] 시리얼 통신 , 패킷 (1) | 2021.01.31 |
|---|
